വാർത്തകൾ - ദ്രാവക ചലനത്തിന്റെ അടിസ്ഥാന ആശയം - ദ്രാവക ചലനാത്മകതയുടെ തത്വങ്ങൾ എന്തൊക്കെയാണ്

ആമുഖം

മുൻ അധ്യായത്തിൽ, നിശ്ചലാവസ്ഥയിലുള്ള ദ്രാവകങ്ങൾ പ്രയോഗിക്കുന്ന ബലങ്ങൾക്ക് കൃത്യമായ ഗണിത സാഹചര്യങ്ങൾ എളുപ്പത്തിൽ ലഭിക്കുമെന്ന് കാണിച്ചുതന്നു. കാരണം, ഹൈഡ്രോസ്റ്റാറ്റിക് സംവിധാനത്തിൽ ലളിതമായ മർദ്ദ ശക്തികൾ മാത്രമേ ഉൾപ്പെട്ടിട്ടുള്ളൂ. ചലനത്തിലുള്ള ഒരു ദ്രാവകം പരിഗണിക്കുമ്പോൾ, വിശകലനത്തിന്റെ പ്രശ്നം ഉടനടി കൂടുതൽ ബുദ്ധിമുട്ടായിത്തീരുന്നു. കണികാ പ്രവേഗത്തിന്റെ വ്യാപ്തിയും ദിശയും കണക്കിലെടുക്കേണ്ടതുണ്ട്, മാത്രമല്ല, ചലിക്കുന്ന ദ്രാവക കണികകൾക്കിടയിലും അടങ്ങിയിരിക്കുന്ന അതിരുകളിലും ഒരു ഷിയർ അല്ലെങ്കിൽ ഘർഷണ സമ്മർദ്ദത്തിന് കാരണമാകുന്ന വിസ്കോസിറ്റിയുടെ സങ്കീർണ്ണമായ സ്വാധീനവുമുണ്ട്. ദ്രാവക ശരീരത്തിന്റെ വ്യത്യസ്ത ഘടകങ്ങൾക്കിടയിൽ സാധ്യമാകുന്ന ആപേക്ഷിക ചലനം, പ്രവാഹ സാഹചര്യങ്ങൾക്കനുസരിച്ച് ഒരു ബിന്ദുവിൽ നിന്ന് മറ്റൊന്നിലേക്ക് മർദ്ദവും ഷിയർ സമ്മർദ്ദവും ഗണ്യമായി വ്യത്യാസപ്പെടാൻ കാരണമാകുന്നു. പ്രവാഹ പ്രതിഭാസവുമായി ബന്ധപ്പെട്ട സങ്കീർണ്ണതകൾ കാരണം, കൃത്യമായ ഗണിത വിശകലനം ചുരുക്കം ചില കേസുകളിൽ മാത്രമേ സാധ്യമാകൂ, എഞ്ചിനീയറിംഗ് വീക്ഷണകോണിൽ നിന്ന്, ചിലത് പ്രായോഗികമല്ല. അതിനാൽ, പരീക്ഷണത്തിലൂടെയോ അല്ലെങ്കിൽ ഒരു സൈദ്ധാന്തിക പരിഹാരം ലഭിക്കുന്നതിന് പര്യാപ്തമായ ചില ലളിതവൽക്കരണ അനുമാനങ്ങൾ നടത്തിക്കൊണ്ടോ ഒഴുക്ക് പ്രശ്നങ്ങൾ പരിഹരിക്കേണ്ടത് ആവശ്യമാണ്. മെക്കാനിക്സിന്റെ അടിസ്ഥാന നിയമങ്ങൾ എല്ലായ്പ്പോഴും സാധുതയുള്ളതും നിരവധി പ്രധാനപ്പെട്ട സന്ദർഭങ്ങളിൽ ഭാഗികമായി സൈദ്ധാന്തിക രീതികൾ സ്വീകരിക്കാൻ പ്രാപ്തമാക്കുന്നതുമായതിനാൽ രണ്ട് സമീപനങ്ങളും പരസ്പരം വിരുദ്ധമല്ല. ലളിതമായ വിശകലനത്തിന്റെ ഫലമായി യഥാർത്ഥ അവസ്ഥകളിൽ നിന്നുള്ള വ്യതിയാനത്തിന്റെ വ്യാപ്തി പരീക്ഷണാത്മകമായി കണ്ടെത്തേണ്ടതും പ്രധാനമാണ്.

ദ്രാവകം ആദർശപരമോ പൂർണ്ണമോ ആണെന്നും അതുവഴി സങ്കീർണ്ണമായ വിസ്കോസ് ഇഫക്റ്റുകൾ ഇല്ലാതാക്കുന്നുവെന്നുമാണ് ഏറ്റവും സാധാരണമായ ലളിതവൽക്കരണ അനുമാനം. സ്റ്റോക്സ്, റെയ്‌ലീ, റാങ്കിൻ, കെൽവിൻ, ലാംബ് തുടങ്ങിയ പ്രഗത്ഭ പണ്ഡിതരുടെ ശ്രദ്ധ നേടിയ പ്രായോഗിക ഗണിതശാസ്ത്ര ശാഖയായ ക്ലാസിക്കൽ ഹൈഡ്രോഡൈനാമിക്സിന്റെ അടിസ്ഥാനമാണിത്. ക്ലാസിക്കൽ സിദ്ധാന്തത്തിൽ ഗുരുതരമായ അന്തർലീനമായ പരിമിതികളുണ്ട്, പക്ഷേ ജലത്തിന് താരതമ്യേന കുറഞ്ഞ വിസ്കോസിറ്റി ഉള്ളതിനാൽ, അത് പല സാഹചര്യങ്ങളിലും ഒരു യഥാർത്ഥ ദ്രാവകമായി പ്രവർത്തിക്കുന്നു. ഇക്കാരണത്താൽ, ദ്രാവക ചലനത്തിന്റെ സവിശേഷതകളെക്കുറിച്ചുള്ള പഠനത്തിന് ക്ലാസിക്കൽ ഹൈഡ്രോഡൈനാമിക്സിനെ ഏറ്റവും വിലപ്പെട്ട പശ്ചാത്തലമായി കണക്കാക്കാം. ദ്രാവക ചലനത്തിന്റെ അടിസ്ഥാന ചലനവുമായി ബന്ധപ്പെട്ടതാണ് ഈ അധ്യായം, സിവിൽ എഞ്ചിനീയറിംഗ് ഹൈഡ്രോളിക്സിൽ നേരിടുന്ന കൂടുതൽ നിർദ്ദിഷ്ട പ്രശ്നങ്ങൾ കൈകാര്യം ചെയ്യുന്ന തുടർന്നുള്ള അധ്യായങ്ങളിലേക്കുള്ള ഒരു അടിസ്ഥാന ആമുഖമായി ഇത് പ്രവർത്തിക്കുന്നു. ദ്രാവക ചലനത്തിന്റെ മൂന്ന് പ്രധാന അടിസ്ഥാന സമവാക്യങ്ങളായ തുടർച്ച, ബെർണൂലി, മൊമെന്റം സമവാക്യങ്ങൾ എന്നിവ ഉരുത്തിരിഞ്ഞുവന്നതും അവയുടെ പ്രാധാന്യം വിശദീകരിക്കുന്നതും ആണ്. പിന്നീട്, ക്ലാസിക്കൽ സിദ്ധാന്തത്തിന്റെ പരിമിതികൾ പരിഗണിക്കുകയും ഒരു യഥാർത്ഥ ദ്രാവകത്തിന്റെ സ്വഭാവം വിവരിക്കുകയും ചെയ്യുന്നു. ഒരു അപൂർണ്ണമായ ദ്രാവകം മുഴുവൻ അനുമാനിക്കപ്പെടുന്നു.

ഒഴുക്കിന്റെ തരങ്ങൾ

വിവിധ തരം ദ്രാവക ചലനങ്ങളെ ഇനിപ്പറയുന്ന രീതിയിൽ തരംതിരിക്കാം:

1.പ്രക്ഷുബ്ധവും ലാമിനാറും

2. ഭ്രമണപരവും അരോട്ടേഷനും

3. സ്ഥിരതയുള്ളതും അസ്ഥിരവുമായത്

4. യൂണിഫോമും അല്ലാത്തതും.

സബ്‌മെർസിബിൾ മലിനജല പമ്പ്

എംവിഎസ് സീരീസ് ആക്സിയൽ-ഫ്ലോ പമ്പുകൾ എവിഎസ് സീരീസ് മിക്സഡ്-ഫ്ലോ പമ്പുകൾ (ലംബ ആക്സിയൽ ഫ്ലോ, മിക്സഡ് ഫ്ലോ സബ്‌മെർസിബിൾ സീവേജ് പമ്പ്) വിദേശ ആധുനിക സാങ്കേതികവിദ്യ സ്വീകരിച്ചുകൊണ്ട് വിജയകരമായി രൂപകൽപ്പന ചെയ്ത ആധുനിക ഉൽ‌പാദനങ്ങളാണ്. പുതിയ പമ്പുകളുടെ ശേഷി പഴയതിനേക്കാൾ 20% കൂടുതലാണ്. കാര്യക്ഷമത പഴയതിനേക്കാൾ 3~5% കൂടുതലാണ്.

പ്രക്ഷുബ്ധവും ലാമിനാർ പ്രവാഹവും.

ഈ പദങ്ങൾ ഒഴുക്കിന്റെ ഭൗതിക സ്വഭാവത്തെ വിവരിക്കുന്നു.

പ്രക്ഷുബ്ധമായ പ്രവാഹത്തിൽ, ദ്രാവക കണികകളുടെ പുരോഗതി ക്രമരഹിതമാണ്, കൂടാതെ സ്ഥാനത്തിന്റെ ഒരു ക്രമരഹിതമായ കൈമാറ്റം സംഭവിക്കുന്നു. വ്യക്തിഗത കണികകൾ ചാഞ്ചാട്ടമുള്ള ട്രാൻസ്. വെഴ്‌സ് പ്രവേഗങ്ങൾക്ക് വിധേയമാണ്, അതിനാൽ ചലനം നേർരേഖയ്ക്ക് പകരം ചുഴലിക്കാറ്റും സൈനസും ആയിരിക്കും. ഒരു പ്രത്യേക ഘട്ടത്തിൽ ചായം കുത്തിവച്ചാൽ, അത് ഒഴുക്ക് പ്രവാഹത്തിലുടനീളം വേഗത്തിൽ വ്യാപിക്കും. ഉദാഹരണത്തിന്, ഒരു പൈപ്പിലെ പ്രക്ഷുബ്ധമായ പ്രവാഹത്തിന്റെ കാര്യത്തിൽ, ഒരു വിഭാഗത്തിലെ പ്രവേഗത്തിന്റെ ഒരു തൽക്ഷണ റെക്കോർഡിംഗ് ചിത്രം 1(a) ൽ കാണിച്ചിരിക്കുന്നതുപോലെ ഒരു ഏകദേശ വിതരണം വെളിപ്പെടുത്തും. സാധാരണ അളക്കൽ ഉപകരണങ്ങൾ രേഖപ്പെടുത്തുന്നതുപോലെ, സ്ഥിരമായ പ്രവേഗം ഡോട്ട് ചെയ്ത രൂപരേഖയിൽ സൂചിപ്പിച്ചിരിക്കുന്നു, കൂടാതെ ഒരു താൽക്കാലിക സ്ഥിരമായ ശരാശരിയിൽ സൂപ്പർഇമ്പോസ് ചെയ്തിരിക്കുന്ന അസ്ഥിരമായ ചാഞ്ചാട്ട പ്രവേഗമാണ് പ്രക്ഷുബ്ധമായ പ്രവാഹത്തിന്റെ സവിശേഷതയെന്ന് വ്യക്തമാണ്.

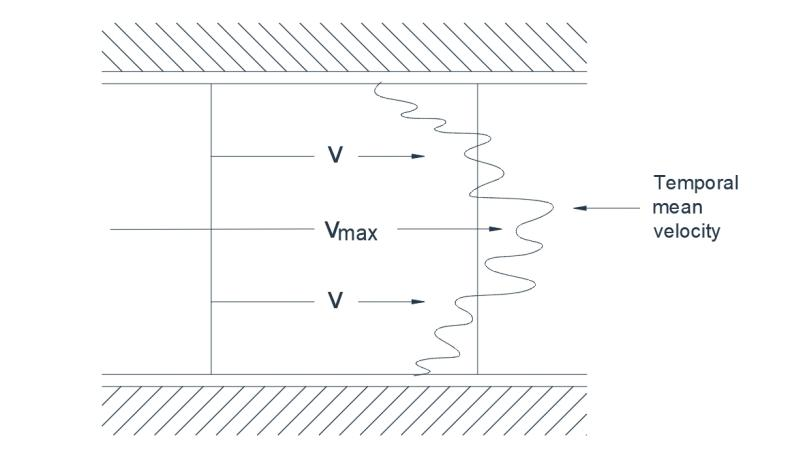
ചിത്രം 1(എ) പ്രക്ഷുബ്ധമായ ഒഴുക്ക്

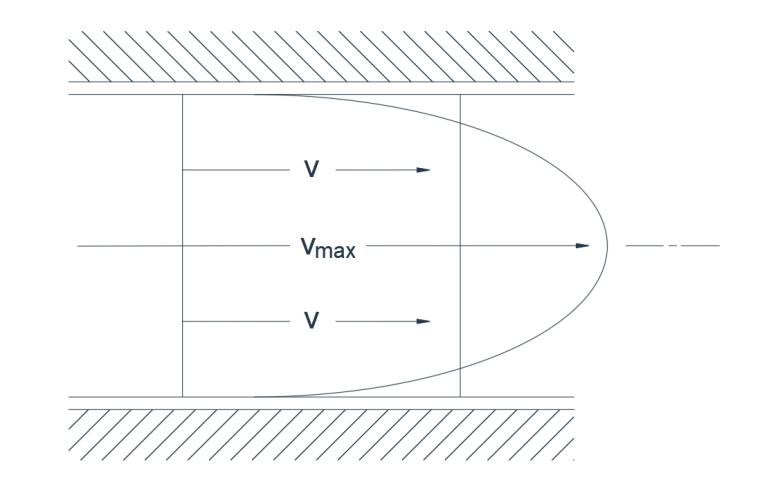
ചിത്രം 1(ബി) ലാമിനാർ ഫ്ലോ

ലാമിനാർ പ്രവാഹത്തിൽ എല്ലാ ദ്രാവക കണികകളും സമാന്തര പാതകളിലൂടെയാണ് സഞ്ചരിക്കുന്നത്, പ്രവേഗത്തിന്റെ ഒരു തിരശ്ചീന ഘടകവുമില്ല. ക്രമീകൃതമായ പുരോഗതി, ഓരോ കണികയും അതിന് മുമ്പുള്ള കണികയുടെ പാതയെ ഒരു വ്യതിയാനവുമില്ലാതെ കൃത്യമായി പിന്തുടരുന്നു എന്നതാണ്. അങ്ങനെ, ഡൈയുടെ ഒരു നേർത്ത ഫിലമെന്റ് വ്യാപനമില്ലാതെ അതേപടി നിലനിൽക്കും. ലാമിനാർ പ്രവാഹത്തിൽ (ചിത്രം 1b) ടർബലന്റ് പ്രവാഹത്തേക്കാൾ വളരെ വലിയ ഒരു തിരശ്ചീന പ്രവേഗ ഗ്രേഡിയന്റ് ഉണ്ട്. ഉദാഹരണത്തിന്, ഒരു പൈപ്പിന്, ശരാശരി പ്രവേഗം V യുടെയും പരമാവധി പ്രവേഗം V യുടെയും അനുപാതം ടർബലന്റ് പ്രവാഹത്തിൽ 0.5 ഉം ലാമിനാർ പ്രവാഹത്തിൽ 0.05 ഉം ആണ്.

ലാമിനാർ പ്രവാഹം കുറഞ്ഞ വേഗതയും വിസ്കോസ് സ്ലഗ്ഗി ഫ്ലൂയിഡുകളുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. പൈപ്പ്‌ലൈനിലും ഓപ്പൺ-ചാനൽ ഹൈഡ്രോളിക്‌സിലും, പ്രക്ഷുബ്ധമായ പ്രവാഹം ഉറപ്പാക്കാൻ വേഗത എപ്പോഴും ആവശ്യത്തിന് ഉയർന്നതാണ്, എന്നിരുന്നാലും ഒരു നേർത്ത ലാമിനാർ പാളി ഒരു ഖര അതിർത്തിയുടെ സമീപത്ത് നിലനിൽക്കുന്നു. ലാമിനാർ പ്രവാഹത്തിന്റെ നിയമങ്ങൾ പൂർണ്ണമായി മനസ്സിലാക്കാം, ലളിതമായ അതിർത്തി വ്യവസ്ഥകൾക്ക് പ്രവേഗ വിതരണം ഗണിതശാസ്ത്രപരമായി വിശകലനം ചെയ്യാൻ കഴിയും. ക്രമരഹിതമായ സ്പന്ദന സ്വഭാവം കാരണം, പ്രക്ഷുബ്ധമായ പ്രവാഹം കർശനമായ ഗണിതശാസ്ത്ര ചികിത്സയെ വെല്ലുവിളിക്കുന്നു, പ്രായോഗിക പ്രശ്‌നങ്ങളുടെ പരിഹാരത്തിന്, അനുഭവപരമോ അർദ്ധാനുഭവപരമോ ആയ ബന്ധങ്ങളെയാണ് പ്രധാനമായും ആശ്രയിക്കേണ്ടത്.

വെർട്ടിക്കൽ ടർബൈൻ ഫയർ പമ്പ്

മോഡൽ നമ്പർ: XBC-VTP

XBC-VTP സീരീസ് വെർട്ടിക്കൽ ലോംഗ് ഷാഫ്റ്റ് ഫയർ ഫൈറ്റിംഗ് പമ്പുകൾ ഏറ്റവും പുതിയ നാഷണൽ സ്റ്റാൻഡേർഡ് GB6245-2006 അനുസരിച്ച് നിർമ്മിച്ച സിംഗിൾ സ്റ്റേജ്, മൾട്ടിസ്റ്റേജ് ഡിഫ്യൂസർ പമ്പുകളുടെ ഒരു പരമ്പരയാണ്. യുണൈറ്റഡ് സ്റ്റേറ്റ്സ് ഫയർ പ്രൊട്ടക്ഷൻ അസോസിയേഷന്റെ നിലവാരത്തിന്റെ റഫറൻസ് ഉപയോഗിച്ച് ഞങ്ങൾ ഡിസൈൻ മെച്ചപ്പെടുത്തി. പെട്രോകെമിക്കൽ, പ്രകൃതിവാതകം, പവർ പ്ലാന്റ്, കോട്ടൺ ടെക്സ്റ്റൈൽ, വാർഫ്, വ്യോമയാനം, വെയർഹൗസിംഗ്, ഉയർന്ന കെട്ടിടങ്ങൾ, മറ്റ് വ്യവസായങ്ങൾ എന്നിവയിലെ അഗ്നി ജലവിതരണത്തിനാണ് ഇത് പ്രധാനമായും ഉപയോഗിക്കുന്നത്. കപ്പൽ, കടൽ ടാങ്ക്, ഫയർ ഷിപ്പ്, മറ്റ് വിതരണ അവസരങ്ങൾ എന്നിവയിലും ഇത് പ്രയോഗിക്കാവുന്നതാണ്.

ഭ്രമണ, അരോചക പ്രവാഹങ്ങൾ.

ഓരോ ദ്രാവക കണികയ്ക്കും അതിന്റേതായ പിണ്ഡകേന്ദ്രത്തെക്കുറിച്ച് ഒരു കോണീയ പ്രവേഗമുണ്ടെങ്കിൽ ആ പ്രവാഹത്തെ ഭ്രമണ പ്രവാഹം എന്ന് വിളിക്കുന്നു.

ചിത്രം 2a ഒരു നേർരേഖയ്ക്ക് അപ്പുറമുള്ള പ്രക്ഷുബ്ധമായ പ്രവാഹവുമായി ബന്ധപ്പെട്ട ഒരു സാധാരണ പ്രവേഗ വിതരണം കാണിക്കുന്നു. ഏകീകൃതമല്ലാത്ത പ്രവേഗ വിതരണം കാരണം, രണ്ട് അക്ഷങ്ങളും യഥാർത്ഥത്തിൽ ലംബമായി സ്ഥിതിചെയ്യുന്ന ഒരു കണികയ്ക്ക് ചെറിയ അളവിലുള്ള ഭ്രമണത്തോടെ രൂപഭേദം സംഭവിക്കുന്നു. ചിത്രം 2a-യിൽ, വൃത്താകൃതിയിലുള്ള ഒഴുക്ക്.

പാത ചിത്രീകരിച്ചിരിക്കുന്നു, പ്രവേഗം ആരത്തിന് നേർ അനുപാതത്തിലാണ്. കണികയുടെ രണ്ട് അക്ഷങ്ങളും ഒരേ ദിശയിൽ കറങ്ങുന്നതിനാൽ പ്രവാഹം വീണ്ടും ഭ്രമണാത്മകമാകും.

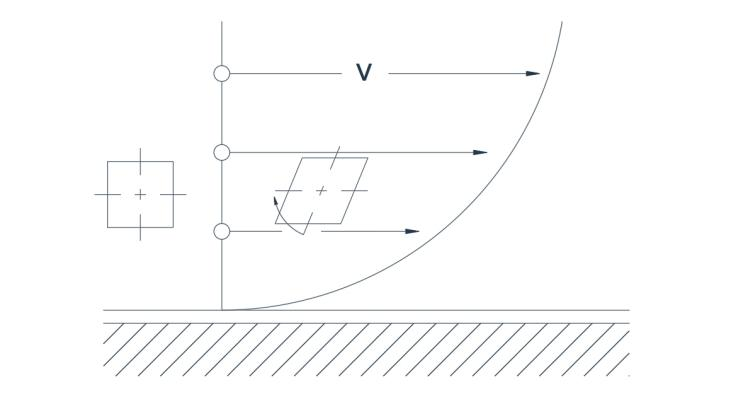
ചിത്രം 2(എ) ഭ്രമണ പ്രവാഹം

പ്രവാഹം ഭ്രമണരഹിതമാകണമെങ്കിൽ, നേർരേഖയോട് ചേർന്നുള്ള പ്രവേഗ വിതരണം ഏകതാനമായിരിക്കണം (ചിത്രം 2b). ഒരു വൃത്താകൃതിയിലുള്ള പാതയിലെ പ്രവാഹത്തിന്റെ കാര്യത്തിൽ, പ്രവേഗം ആരത്തിന് വിപരീത അനുപാതത്തിലാണെങ്കിൽ മാത്രമേ ഭ്രമണപ്രവാഹം ബാധകമാകൂ എന്ന് കാണിക്കാൻ കഴിയും. ചിത്രം 3-ലെ ആദ്യ നോട്ടത്തിൽ, ഇത് തെറ്റാണെന്ന് തോന്നുന്നു, പക്ഷേ സൂക്ഷ്മപരിശോധനയിൽ രണ്ട് അക്ഷങ്ങളും വിപരീത ദിശകളിലേക്ക് കറങ്ങുന്നുവെന്ന് വെളിപ്പെടുത്തുന്നു, അതിനാൽ പ്രാരംഭ അവസ്ഥയിൽ നിന്ന് മാറ്റമില്ലാത്ത അക്ഷങ്ങളുടെ ശരാശരി ഓറിയന്റേഷൻ സൃഷ്ടിക്കുന്ന ഒരു നഷ്ടപരിഹാര പ്രഭാവം ഉണ്ട്.

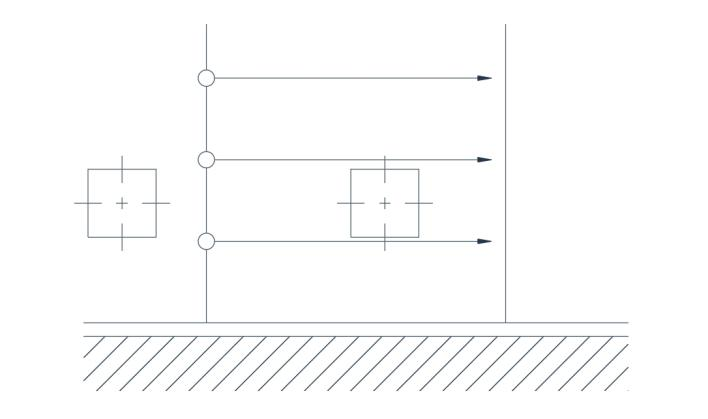
ചിത്രം 2(b) അചഞ്ചലമായ പ്രവാഹം

എല്ലാ ദ്രാവകങ്ങൾക്കും വിസ്കോസിറ്റി ഉള്ളതിനാൽ, ഒരു യഥാർത്ഥ ദ്രാവകത്തിന്റെ താഴ്ന്ന നില ഒരിക്കലും യഥാർത്ഥ അലോസരപ്പെടുത്തൽ അല്ല, ലാമിനാർ പ്രവാഹം തീർച്ചയായും ഉയർന്ന ഭ്രമണപരവുമാണ്. അതിനാൽ അലോസരപ്പെടുത്തൽ പ്രവാഹം ഒരു സാങ്കൽപ്പിക അവസ്ഥയാണ്, അത് അക്കാദമിക് താൽപ്പര്യമുള്ളതായിരിക്കും - പല പ്രക്ഷുബ്ധ പ്രവാഹ സാഹചര്യങ്ങളിലും ഭ്രമണ സവിശേഷതകൾ വളരെ നിസ്സാരമായതിനാൽ അവ അവഗണിക്കപ്പെടാം എന്ന വസ്തുത ഇല്ലായിരുന്നുവെങ്കിൽ മാത്രം. മുമ്പ് പരാമർശിച്ച ക്ലാസിക്കൽ ഹൈഡ്രോഡൈനാമിക്സിന്റെ ഗണിതശാസ്ത്ര ആശയങ്ങൾ ഉപയോഗിച്ച് അലോസരപ്പെടുത്തൽ പ്രവാഹം വിശകലനം ചെയ്യാൻ കഴിയുന്നതിനാൽ ഇത് സൗകര്യപ്രദമാണ്.

സെൻട്രിഫ്യൂഗൽ സീ വാട്ടർ ഡെസ്റ്റിനേഷൻ പമ്പ്

മോഡൽ നമ്പർ: ASN ASNV

മോഡൽ ASN, ASNV പമ്പുകൾ സിംഗിൾ-സ്റ്റേജ് ഡബിൾ സക്ഷൻ സ്പ്ലിറ്റ് വോള്യൂട്ട് കേസിംഗ് സെൻട്രിഫ്യൂഗൽ പമ്പുകളും ജല പ്രവർത്തനങ്ങൾ, എയർ കണ്ടീഷനിംഗ് സർക്കുലേഷൻ, കെട്ടിടം, ജലസേചനം, ഡ്രെയിനേജ് പമ്പ് സ്റ്റേഷൻ, ഇലക്ട്രിക് പവർ സ്റ്റേഷൻ, വ്യാവസായിക ജലവിതരണ സംവിധാനം, അഗ്നിശമന സംവിധാനം, കപ്പൽ, കെട്ടിടം തുടങ്ങിയവയ്ക്കായി ഉപയോഗിച്ചതോ ദ്രാവക ഗതാഗതമോ ആണ്.

സ്ഥിരവും അസ്ഥിരവുമായ ഒഴുക്ക്.

ഏതെങ്കിലും ബിന്ദുവിലെ അവസ്ഥകൾ സമയവുമായി ബന്ധപ്പെട്ട് സ്ഥിരമായിരിക്കുമ്പോൾ ആ ഒഴുക്ക് സ്ഥിരമാണെന്ന് പറയപ്പെടുന്നു. ഈ നിർവചനത്തിന്റെ കർശനമായ വ്യാഖ്യാനം, പ്രക്ഷുബ്ധമായ ഒഴുക്ക് ഒരിക്കലും യഥാർത്ഥത്തിൽ സ്ഥിരമായിരുന്നില്ല എന്ന നിഗമനത്തിലേക്ക് നയിക്കും. എന്നിരുന്നാലും, ഇപ്പോഴത്തെ ആവശ്യത്തിനായി, പൊതുവായ ദ്രാവക ചലനത്തെ മാനദണ്ഡമായും പ്രക്ഷുബ്ധവുമായി ബന്ധപ്പെട്ട ക്രമരഹിതമായ ഏറ്റക്കുറച്ചിലുകളെ ഒരു ദ്വിതീയ സ്വാധീനമായും കണക്കാക്കുന്നത് സൗകര്യപ്രദമാണ്. സ്ഥിരമായ ഒഴുക്കിന്റെ വ്യക്തമായ ഉദാഹരണം ഒരു കുഴലിലോ തുറന്ന ചാനലിലോ ഉള്ള സ്ഥിരമായ ഡിസ്ചാർജ് ആണ്.

ഇതിന്റെ ഫലമായി, സമയത്തിനനുസരിച്ച് സാഹചര്യങ്ങൾ വ്യത്യാസപ്പെടുമ്പോൾ ഒഴുക്ക് അസ്ഥിരമാണെന്ന് ഇത് പിന്തുടരുന്നു. അസ്ഥിരമായ ഒഴുക്കിന് ഒരു ഉദാഹരണം ഒരു കുഴലിലോ തുറന്ന ചാനലിലോ വ്യത്യാസപ്പെടുന്ന ഡിസ്ചാർജ് ആണ്; ഇത് സാധാരണയായി ഒരു സ്ഥിരമായ ഡിസ്ചാർജിന് തുടർച്ചയായി അല്ലെങ്കിൽ തുടർന്ന് സംഭവിക്കുന്ന ഒരു ക്ഷണിക പ്രതിഭാസമാണ്. മറ്റ് പരിചിതമായവ

കൂടുതൽ ആനുകാലിക സ്വഭാവത്തിന്റെ ഉദാഹരണങ്ങളാണ് തരംഗ ചലനവും വേലിയേറ്റ പ്രവാഹത്തിൽ വലിയ ജലാശയങ്ങളുടെ ചാക്രിക ചലനവും.

ഹൈഡ്രോളിക് എഞ്ചിനീയറിംഗിലെ പ്രായോഗിക പ്രശ്നങ്ങളിൽ ഭൂരിഭാഗവും സ്ഥിരമായ പ്രവാഹവുമായി ബന്ധപ്പെട്ടതാണ്. ഇത് ഭാഗ്യകരമാണ്, കാരണം അസ്ഥിരമായ പ്രവാഹത്തിലെ സമയ വേരിയബിൾ വിശകലനത്തെ ഗണ്യമായി സങ്കീർണ്ണമാക്കുന്നു. അതനുസരിച്ച്, ഈ അധ്യായത്തിൽ, അസ്ഥിരമായ പ്രവാഹത്തെക്കുറിച്ചുള്ള പരിഗണന താരതമ്യേന ലളിതമായ ചില കേസുകളിലേക്ക് പരിമിതപ്പെടുത്തും. എന്നിരുന്നാലും, ആപേക്ഷിക ചലന തത്വത്തിന്റെ അടിസ്ഥാനത്തിൽ അസ്ഥിരമായ പ്രവാഹത്തിന്റെ നിരവധി സാധാരണ സംഭവങ്ങൾ സ്ഥിരമായ അവസ്ഥയിലേക്ക് ചുരുക്കപ്പെടാമെന്ന് ഓർമ്മിക്കേണ്ടത് പ്രധാനമാണ്.

അങ്ങനെ, നിശ്ചല ജലത്തിലൂടെ സഞ്ചരിക്കുന്ന ഒരു പാത്രവുമായി ബന്ധപ്പെട്ട ഒരു പ്രശ്നം, പാത്രം നിശ്ചലമായും വെള്ളം ചലനത്തിലുമാകുന്ന തരത്തിലും പുനർനിർമ്മിക്കാവുന്നതാണ്; ദ്രാവക സ്വഭാവത്തിന്റെ സമാനതയ്ക്കുള്ള ഏക മാനദണ്ഡം ആപേക്ഷിക പ്രവേഗം ഒന്നായിരിക്കണമെന്നതാണ്. വീണ്ടും, ആഴത്തിലുള്ള ജലത്തിലെ തരംഗ ചലനം

ഒരു നിരീക്ഷകൻ തരംഗങ്ങളുമായി ഒരേ വേഗതയിൽ സഞ്ചരിക്കുന്നുവെന്ന് അനുമാനിക്കുന്നതിലൂടെ സ്ഥിരമായ അവസ്ഥ നിർണ്ണയിക്കപ്പെടുന്നു.

ലംബ ടർബൈൻ പമ്പ്

ഡീസൽ എഞ്ചിൻ വെർട്ടിക്കൽ ടർബൈൻ മൾട്ടിസ്റ്റേജ് സെൻട്രിഫ്യൂഗൽ ഇൻലൈൻ ഷാഫ്റ്റ് വാട്ടർ ഡ്രെയിനേജ് പമ്പ് ഇത്തരത്തിലുള്ള ലംബ ഡ്രെയിനേജ് പമ്പ് പ്രധാനമായും ഉപയോഗിക്കുന്നത് നാശമില്ലാത്ത പമ്പിംഗിനും, 60 °C-ൽ താഴെയുള്ള താപനിലയ്ക്കും, സസ്പെൻഡ് ചെയ്ത സോളിഡുകൾ (ഫൈബർ, ഗ്രിറ്റുകൾ എന്നിവയല്ലാതെ) 150 mg/L-ൽ താഴെയുള്ള മലിനജലത്തിന്റെയോ മാലിന്യജലത്തിന്റെയോ ഉള്ളടക്കം പമ്പ് ചെയ്യുന്നതിനുമാണ്. VTP തരം ലംബ ഡ്രെയിനേജ് പമ്പ് VTP തരം ലംബ വാട്ടർ പമ്പുകളിലാണ്, വർദ്ധനവിന്റെയും കോളറിന്റെയും അടിസ്ഥാനത്തിൽ, ട്യൂബ് ഓയിൽ ലൂബ്രിക്കേഷൻ വെള്ളമാണെന്ന് സജ്ജമാക്കുക. 60 °C-ൽ താഴെയുള്ള താപനില പുകയാൻ കഴിയും, ഒരു നിശ്ചിത ഖര ധാന്യം (സ്ക്രാപ്പ് ഇരുമ്പ്, നേർത്ത മണൽ, കൽക്കരി മുതലായവ) മലിനജലമോ മാലിന്യജലമോ ഉൾക്കൊള്ളാൻ അയയ്ക്കാം.

ഏകീകൃതവും ഏകീകൃതമല്ലാത്തതുമായ ഒഴുക്ക്.

ഒരു ബിന്ദുവിൽ നിന്ന് മറ്റൊന്നിലേക്കുള്ള പ്രവേഗ വെക്റ്ററിന്റെ വ്യാപ്തിയിലും ദിശയിലും പ്രവാഹത്തിന്റെ പാതയിൽ വ്യത്യാസമില്ലെങ്കിൽ പ്രവാഹം ഏകീകൃതമാണെന്ന് പറയപ്പെടുന്നു. ഈ നിർവചനം പാലിക്കുന്നതിന്, ഓരോ ക്രോസ്-എക്ഷനിലും പ്രവാഹത്തിന്റെ വിസ്തീർണ്ണവും പ്രവേഗവും ഒരുപോലെയായിരിക്കണം. പ്രവേഗ വെക്റ്റർ സ്ഥാനത്തിനനുസരിച്ച് വ്യത്യാസപ്പെടുമ്പോൾ ഏകീകൃതമല്ലാത്ത പ്രവാഹം സംഭവിക്കുന്നു, ഒരു സാധാരണ ഉദാഹരണം ഒത്തുചേരുന്നതോ വ്യതിചലിക്കുന്നതോ ആയ അതിരുകൾക്കിടയിലുള്ള പ്രവാഹമാണ്.

ഈ രണ്ട് ഇതര ഒഴുക്ക് സാഹചര്യങ്ങളും തുറന്ന ചാനൽ ഹൈഡ്രോളിക്സിൽ സാധാരണമാണ്, കർശനമായി പറഞ്ഞാൽ, ഏകീകൃതമായ ഒഴുക്ക് എല്ലായ്പ്പോഴും അസിംപ്റ്റോട്ടിക്കലായി സമീപിക്കുന്നതിനാൽ, ഇത് ഒരു ആദർശ അവസ്ഥയാണ്, അത് ഒരിക്കലും യഥാർത്ഥത്തിൽ കൈവരിക്കപ്പെടുന്നില്ല. സാഹചര്യങ്ങൾ സമയവുമായി ബന്ധപ്പെട്ടതല്ല, സ്ഥലവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നുവെന്നും അതിനാൽ അടച്ച ഒഴുക്കിന്റെ സന്ദർഭങ്ങളിൽ (ഉദാ. സമ്മർദ്ദത്തിലുള്ള പൈപ്പുകൾ), അവ ഒഴുക്കിന്റെ സ്ഥിരമായതോ അസ്ഥിരമായതോ ആയ സ്വഭാവത്തിൽ നിന്ന് തികച്ചും സ്വതന്ത്രമാണെന്നും ശ്രദ്ധിക്കേണ്ടതാണ്.

പോസ്റ്റ് സമയം: മാർച്ച്-29-2024